Calculation of Decay Activity of One Gram of Natural Uranium

Problem

How many atoms decay each second in a 1.000 gram sample of natural uranium?

Solution

Short answer: 12,000 atoms per second (12 kBq) if you consider uranium-238 alone; 25,000 atoms per second (25 kBq) if you consider all the uranium isotopes present in natural uranium; or 50,000 atoms per second (50 kBq) if you also consider the decay products that accumulate over the course of a few months or longer following extraction from the uranium ore.

Detailed Calculation

Natural uranium consists of the following isotopes:

Uranium isotope	Percentage	Half-life
uranium-238	99.275%	4.47 billion years
uranium-235	0.720%	704 million years
uranium-234	0.00548%	245 thousand years

 
Note: The numbers don't add up to exactly 100 percent due to rounding.

Let's consider the uranium-238 by itself first, since it makes up more than 99% of natural uranium.

Decay of uranium-238 alone

The 1.000 gram of uranium contains 0.993 gram of uranium-238.

Uranium-238 has a half-life of 4.47 billion years. Let's convert that to seconds:

  (4.47 x 10⁹ years) x (365.25 days/year) x (24 hours/day) x (60 minutes/hour) x (60 seconds/minute) = 1.411 x 10¹⁷ seconds

The get the mean lifetime of a radioactive isotope, designated τ (Greek letter tau), divide the half-life by the natural logarithm of 2:

mean lifetime  τ  = half-life / ln(2) = (1.411 x 10¹⁷ seconds) / 0.6931 = 2.035 x 10¹⁷ seconds

The decay rate, designated λ (Greek letter lambda), is the fraction of the total mass that decays in one unit of time. It is equal to the inverse of the mean lifetime:

  decay rate  λ =  1/τ  =  1 / (2.035 x 10¹⁷ seconds)  =  4.914 x 10^-18 per second

This is the fraction of the uranium-238 that decays in one second, so a mass of 0.993 gram of uranium decays at a rate of 0.993 x 4.914 x 10^-18 = 4.88 x 10^-18 gram per second. To convert this decay rate from grams per second to atoms per second, you use the atomic mass of uranium-238, 238 grams per mole, and the Avogadro constant, 6.022 x 10²³ atoms per mole:

  (4.88 x 10^-18 gram / second) x (1.0 mole / 238 grams) x (6.022 x 10²³ atoms / mole)  =  1.23 x 10⁴ atoms/second

This is 12,300 atoms/second or 12,300 becquerels (12.3 kBq)

Decay rate of uranium-235 alone

The 1.000 gram of uranium contains 0.0072 gram of uranium-235.

Uranium-235 has a half-life of 704 million years. Let's convert that to seconds:

  (704 x 10⁶ years) x (365.25 days/year) x (24 hours/day) x (60 minutes/hour) x (60 seconds/minute) = 2.22 x 10¹⁶ seconds

  mean lifetime  τ  = half-life / ln(2) = (2.22 x 10¹⁶ seconds) / 0.6931 = 3.205 x 10¹⁶ seconds

  decay rate  λ =  1/τ  =  1 / (3.205 x 10¹⁶ seconds)  =  3.12 x 10^-17 per second

The decay rate of 0.0072 gram of uranium-235 is:

  (0.0072 gram) x (3.12 x 10^-17 per second) x (1.0 mole / 235 grams) x (6.022 x 10²³ atoms / mole)  =  570 atoms/second 

This is 570 atoms/second or 570 becquerels.

Decay rate of uranium-234 alone

The 1.000 gram of uranium contains 5.48 x 10^-5 gram of uranium-234.

Uranium-234 has a half-life of 245 thousand years. Let's convert that to seconds:

  (245 x 10³ years) x (365.25 days/year) x (24 hours/day) x (60 minutes/hour) x (60 seconds/minute) = 7.73 x 10¹² seconds

  mean lifetime  τ  = half-life / ln(2) = (7.73 x 10¹² seconds) / 0.6931 = 1.115 x 10¹³ seconds

  decay rate  λ =  1/τ  =  1 / (1.115 x 10¹³ seconds)  =  8.97 x 10^-14 per second

The decay rate of 5.48 x 10^-5 gram of uranium-235 is:

  (5.48 x 10^-5 gram) x ( 8.97 x 10^-14 per second) x (1.0 mole / 234 grams) x (6.022 x 10²³ atoms / mole)    =  12,600 atoms/second

This is 12,600 atoms/second or 12,600 becquerels (12.6 kBq)

Decay rate of natural uranium per gram

The total decay activity for the three uranium isotopes (U-238, U-235, and U-234) in one gram of natural uranium is:

 12.3 kBq + 0.570 kBq + 12.6 kBq = 25.5 kBq

Note: Your answer might be slightly different due to rounding errors.

Relationship between uranium-238 and uranium-234 decay rates

You might be surprised to find that nearly half of the decay activity comes from uranium-234, which makes up only 1/200 of 1% of the total amount of uranium. The reason is that it has a much shorter half-life, just 245,000 years compared to 4.5 billion years for uranium-238, so it decays much faster.

You might also notice the similar decay rates of uranium-238 and uranium-234, both around 12 kBq per gram of natural uranium. This is not a coincidence. Uranium-234 exists in nature only because it is a product in the decay chain of uranium-238. A gram of uranium-238 decays at a rate of 12 kBq, producing thorium-234 at a rate of 12 kBq, which decays into protactinium-234, which decays into uranium-234, and so on. Each nuclide in the decay chain accumulates to an equilibrium concentration such that it is produced at, and decays away at, the same rate as the ultimate ancestor nuclide, uranium-238. (The results obtained in the calculations above are slightly different due to rounding errors.)

Uranium-235, on the other hand, is a primordial nuclide like uranium-238. It exists in nature because is was created when the Earth was formed and has a long enough half-life that it still exists today, 4.5 billion years later. There is no particular relationship between the decay rates of  uranium-235 and uranium-238. Because uranium-235 has a shorter half -life than uranium-238, its relative concentration in natural uranium decreases over geological time spans.

Decay of uranium decay-chain products

The answer obtained earlier for the activity of natural uranium, about 25 kBq per gram, is correct for natural uranium freshly extracted from uranium ore. However, that's not the end of the story. As uranium decays, its decay products begin to accumulate and they themselves begin to decay, thereby increasing the total activity of the material significantly, even after just a few weeks.

Let's take a look at the primary decay products and half-lives of the first few nuclides in the uranium-238 decay chain:

Nuclide	Half-life	Decay product
uranium-238	4.47 billion years	thorium-234
thorium-234	24.1 days	protactinium-234
protactinium-234	1.16 minutes	uranium-234
uranium-234	245,000 years	thorium-230
thorium-230	75,400 years	radium-226
radium-226	1,600 years	radon-222
... and so on ...

In undisturbed natural uranium ore, before the uranium is extracted, all of the decay-chain products of uranium-238 have accumulated to their equilibrium concentrations over geological time periods, such that they are all are being produced, and are decaying away, at the same rate, as determined by the amount and  half-life of the ultimate ancestor nuclide, uranium-238. The equilibrium quantity of each nuclide is inversely proportional to its half-life.

Nuclide	Half-life	Quantity present	Decay rate
uranium-238	4.47 billion years	1/238 mole	12.3 kBq
thorium-234	24.1 days	1/238 mole x (1.48 x 10-11)	12.3 kBq
protactinium-234	1.16 minutes	1/238 mole x (4.93 x 10-16)	12.3 kBq
uranium-234	245,000 years	1/238 mole x (5.48 x 10-5)	12.3 kBq
thorium-230	75,400 years	1/238 mole x (1.69 x 10-5)	12.3 kBq
radium-226	1,600 years	1/238 mole x (6.53 x 10-7)	12.3 kBq
... and so on ...

In the Quantity present column above, the number in parentheses is the half-life of the nuclide divided by the half-life of the ultimate ancestor nuclide, uranium-238. For example, the amount of thorium-230 present under equilibrium conditions is 1.0/238 mole (the amount of the ancestor uranium-238 present) multiplied by the ratio of the two half-lives (75,400 / 4,470,000,000 = .0000169).


When uranium is extracted chemically from the ore, all the uranium isotopes are retained, and all the decay products are left behind in the waste product, the mill tailings. The following table shows what the extracted uranium contains (not including the uranium-235, which we will consider later).

Nuclide	Half-life	Quantity present	Decay rate
uranium-238	4.47 billion years	1/238 mole	12.3 kBq
thorium-234	24.1 days	none	none
protactinium-234	1.16 minutes	none	none
uranium-234	245,000 years	1/238 mole x (5.48 x 10-5)	12.3 kBq
thorium-230	75,400 years	none	none
radium-226	1,600 years	none	none
... and so on ...

However, thorium-234 immediately begins to accumulate as the decay product of uranium-238 and itself begins to decay. Because it is being produced at a constant rate (12,300 atoms per second), and its own decay rate is proportional to the amount present, it accumulates to one-half its equilibrium amount in one half-life, to three-fourths of that amount in two half-lives, to seven-eights of that amount in three half-lives, and so on.

Therefore, after one half-life (24 days), we have the following amounts of uranium-238 decay-chain products.

Nuclide	Half-life	Quantity present	Decay rate
uranium-238	4.47 billion years	1/238 mole	12.3 kBq
thorium-234	24.1 days	1/238 mole x (1.48 x 10-11) x 0.5	6.1 kBq
protactinium-234	1.16 minutes	1/238 mole x (4.93 x 10-16) x 0.5	6.1 kBq
uranium-234	245,000 years	1/238 mole x (5.48 x 10-5)	12.3 kBq
thorium-230	75,400 years	negligible	none
radium-226	1,600 years	none	none
... and so on ...

Protactinium-234 has a half-life of one minute, so it decays just about as fast as it is produced. So it also reaches one-half of its equilibrium amount in 24 days, because it is being produced at one-half its equilibrium rate. Thorium-230 is also accumulating at 12,300 atoms per second as a decay product of uranium-234. However, because thorium-230 has such a long half-life on a human time scale (75,400 years), it can be considered, for practical purposes, a stable element that accumulates without decay. As a result, none of the decay-chain nuclides below thorium-230, such as radium and radon, will be produced in the next several tens of thousands of years.


By the time a few months have passed, thorium-234 and protactinium-234 accumulate to their equilibrium amounts and decay at the same equilibrium rate of 12.3 kBq.

Nuclide	Half-life	Quantity present	Decay rate
uranium-238	4.47 billion years	1/238 mole	12.3 kBq
thorium-234	24.1 days	1/238 mole x (1.48 x 10-11)	12.3 kBq
protactinium-234	1.16 minutes	1/238 mole x (4.93 x 10-16)	12.3 kBq
uranium-234	245,000 years	1/238 mole x (5.48 x 10-5)	12.3 kBq
thorium-230	75,400 years	negligible	none
radium-226	1,600 years	none	none
... and so on ...

Therefore, total activity of uranium-238 and uranium-234, as long as it has been sitting around for a few months or more after extraction from the ore, has an activity of 4 x 12.3 kBq = 49.2 kBq.

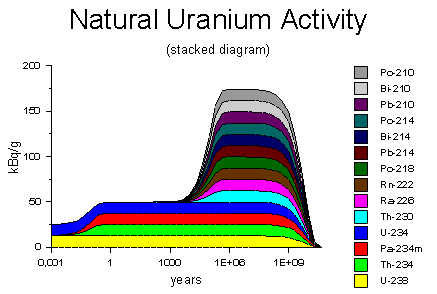The diagram on the right shows the decay activity of one gram of natural uranium on the logarithmic time scale, ranging from 3 days to 30 billion years. When freshly extracted from the ore, the uranium has an decay rate of 25 kBq, arising equally from the uranium-238 and uranium-234. Within a few months, the decay products thorium-234 and protactinium-234 accumulate to their equilibrium concentrations, doubling the activity to 50 kBq. The activity remains constant for tens of thousands of years, until the thorium-230 has a chance to accumulate to significant levels. After that, all of the decay-chain nuclides accumulate to their equilibrium levels, in what is called secular equilibrium, or equilibrium over the ages. This is what you see in old uranium ore rocks. Eventually, after tens of billions of years, the uranium-238 will run out and all activity will die away. Diagram source: WISE Uranium Project, Uranium Radiation Properties

Meanwhile, the small amount of uranium-235 in natural uranium also produces a nuclide that contributes to the total activity. A similar consideration of the uranium-235 decay-chain produces the following results.

Nuclide	Half-life	Quantity present	Decay rate
uranium-235	704 million years	0.0072 / 235 mole	570 Bq
thorium-231	25.52 hours	0.0072 / 235 mole x (4.1 x 10-12)	570 Bq
protactinium-231	32,800 years	negligible	none
actinium-227	21.8 years	none	none
thorium-227	18.7 days	none	none
radium-223	11.4 days	none	none
... and so on ...

Thus, the activity of one gram of natural uranium due to the presence of uranium-235 that has been sitting around for a few days or more is 2 x 570 Bq = 1,140 Bq = 1.14 kBq.

The final answer

The total activity of one gram of natural uranium that has been sitting around for a few months or longer is the activity of uranium-238 and its decay products thorium-234, protactinium-234, and uranium-234 (49.2 kBq); plus the activity of the 0.72% of uranium-235 present and its decay product thorium-231 (1.1 kBq). Thus, the total activity is 50.3 kBq per gram of natural uranium.
 

Why is the decay of uranium isotopes important?

Shortly after the discovery of radioactivity by Henri Becquerel in 1896, Marie Curie found that only uranium and thorium were radioactive among the known elements. She also found that the form of uranium, whether pure metal, uranium salt, or uranium oxide, made no difference in the strength of the radioactivity. Only the amount of uranium present was important, with one exception -- pitchblende ore was four times more radioactive than expected for its uranium content.

Curie correctly hypothesized that the extra radioactivity was caused by the presence of undiscovered radioactive elements, present in small quantities but with greater activity that uranium. By separating pitchblende ore into is constituent parts, she discovered two new elements, polonium and radium, which are decay-chain products of uranium-238.


In assessing the environmental dangers of uranium mining, one must consider not only the uranium extracted from the ore, but also the leftover waste rock left behind after extraction, the mill tailings, which are more radioactive than the uranium itself. For more information on this subject, see Peter Diehl's Uranium Radiation Properties web page and its top-level index page, the World Information Service on Energy Uranium Project.


Among the isotopes of natural uranium, only uranium-235 is fissile, that is, can be used in nuclear reactors or to make nuclear weapons. For these purposes, the uranium must be enriched from the natural 0.72% concentration to at least 3% for nuclear fuel or at least 90% for nuclear weapons.

Because all isotopes of uranium are chemically identical, the only way to separate out the uranium-235 from uranium-238 is to take advantage of the small difference in mass of the two nuclides. In the modern gas centrifuge method, a gaseous compound of uranium is spun in a rapidly rotating cylinder, causing the heavier uranium-238 molecules to accumulate at the outside, forcing the lighter uranium-235 molecules to the inside.

The uranium from which most of the uranium-235 isotope has been removed is called depleted uranium, which has several practical uses but can be dangerous because it is radioactive, and the radioactivity grows over time. It is also toxic in the same way as lead or cadmium.

Back to Radioactive Decay Problem Examples