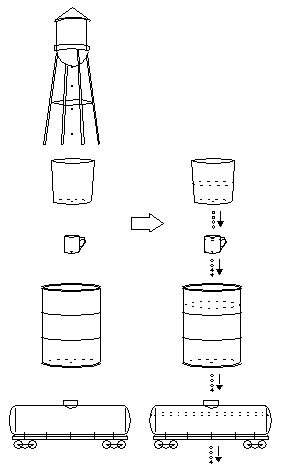
Secular Equilibrium and Radioactive Decay Chains
In a radioactive decay chain, a long-lived ancestor element decays into another element, which itself decays into another element, and so on, resulting in a chain of transformations ending with the formation of a stable element.
In an undisturbed sample of the ancestor element, after enough time has passed, each intermediate decay-chain product accumulates to an equilibrium concentration, such that the element is created at, and decays away at, the same rate. This rate is the same rate for all elements in the chain. The equilibrium amount of each element is proportional to its half-life. This condition is called secular equilibrium, or equilibrium over the ages.
For example, in a sample of uranium ore rock containing 1.00 gram of uranium, the uranium-238 decays at a rate of 12,300 atoms per second into throium-234. The thorium-234 in the rock also decays at a rate of 12,300 atoms per second into protactinium-234. The protactinium-234 in the rock also decays at a rate of 12,300 atoms per second into uranium-234, and so on down the chain, which ends with lead-206, a stable element that accumulates at a rate of 12,300 atoms per second, without any further decay.
238U -> 234Th -> 234Pa -> 234U -> 230Th -> 226Ra -> 222Rn -> 218Po -> 214Pb -> 214Bi -> 214Po -> 210Pb -> 210Bi -> 201Po -> 206Pb
What causes this exquisite match-up in decay rates for all the elements in the decay chain? The answer lies in the behavior of all radioactive materials -- the decay rate is proportional to the amount of material present. So when a long-lived ancestor element decays at a constant rate, each descendent eventually accumulates to the level at which it decays at the same rate as it is produced. This concept is easier to understand when you consider the analogy described in the next section.
| First, a brief note on terminology. So far, I've used the term element to describe a distinctive radioactive material. However, this term does not distinguish between different isotopes of the same element, for example, uranium-238 and uranuim-234. The word isotope
can be used to describe different radioactive forms of the same
element, but not different elements, such as uranium-238 and its decay
product thorium-234. Therefore, I'll use the less common term nuclide
to describe an "atomic species," that is, an atom with a nucleus having
a given number of protons and a given number of neutrons. |
The Dripping Bucket Analogy
 Imagine that you have the job of maintaining your city's water
supply tower, a huge tank carrying enough water to supply the whole
city. On your first day of work, you notice that water is leaking from
the tank and dripping on the ground -- drip, drip, drip, drip -- at a
steady 4 drops per second.
Imagine that you have the job of maintaining your city's water
supply tower, a huge tank carrying enough water to supply the whole
city. On your first day of work, you notice that water is leaking from
the tank and dripping on the ground -- drip, drip, drip, drip -- at a
steady 4 drops per second. You hate to see water being wasted and making a messy puddle, so you find a bucket to catch the water. Unfortunately, the bucket has a tiny hole on the bottom. You wonder how well this bucket will hold up. As an experiment, you fill it with water and check underneath.
When the bucket is full, it leaks and drips at a rate of 10 drops per second. When the bucket is half full, it drips at a rate of 5 drops per second. When the bucket is nearly empty, it hardly drips at all. After further testing, you discover that the bucket always leaks at a rate proportional to the amount of water in the bucket.
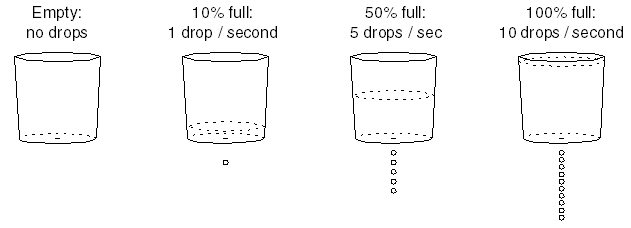
Water enters the bucket at a rate of 4 drops per second. A first, nothing leaks from the bucket, so the water accumulates at a rate of 4 drops per second. However, as the bucket starts filling up, it starts leaking, very slowly at first: drip, ... , drip, ... Remember that the bucket's drip rate is proportional to its fullness.
When the bucket is 10% full, it's losing water at a rate of 1 drop per second out of the bottom, while water enters at a rate of 4 drops per second. So it still has a net accumulation rate of 3 drops per second. So it's still filling up, but more slowly.
When the bucket it 20% full, it's losing water at a rate of 2 drop per second out of the bottom, so it still has a net accumulation rate of 2 drops per second. It's still filling up, but even more slowly.
When the bucket it 30% full, it's losing water at a rate of 3 drop per second out of the bottom, so it still has a net accumulation rate of 1 drop per second. It's still filling up, but even more slowly.
Let's say that you observe the following behavior.
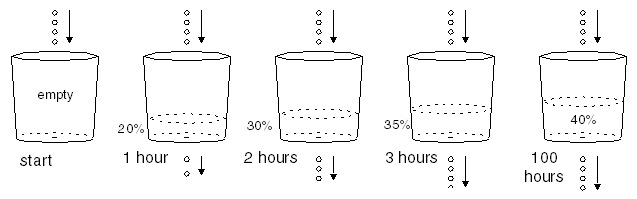
The amount of time it takes for the bucket to fill to one-half the equilibrium level is the half-life of the bucket, which is one hour for this particular bucket, with this particular leaking hole. This becomes apparent when you remove the bucket from the dripping water supply and allow it to drain out through the hole. It starts dripping at 4 drops per second and gradually slows down as the bucket empties. As each hour goes by, the bucket contains half as much water as it did an hour earlier.
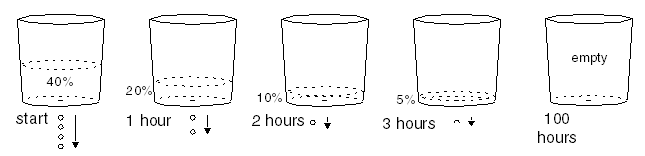
|
An Interesting Note
If you superimpose the picture above (buckets leaking out water) with the previous picture (buckets being being filled from above while also leaking), you'll notice that all five buckets look the same: each has 4 drops per second entering, a total of 4 drops per second leaking out, and a total water level at 40% full. More about this later. |
| For the Mathematically Inclined (skip this box otherwise) Because the amount of water in the tower is very large, the few drips leaking out if it won't affect the total stored amount significantly. Therefore, we can consider the drip rate into the bucket to be a constant, 4 drops per second. When the bucket is catching this water, the amount of water in the bucket as function of time is: x(t) = x(final) + [x(initial) - x(final)] e -λt where x(final) is the final equilibrium amount in the bucket, x(initial) is the starting amount in the bucket, and λ (Greek letter lambda) is the decay constant for the bucket, expressed as the number of drops per unit of time leaking from the bucket divided by the number of drops in the bucket. (For the derivation of this equation, see the Wikipedia article on radioactive decay rates.) For this particular bucket, the half-life is 1.0 hour. The mean lifetime τ (Greek letter tau) (1/e life) is the half-life divided by the natural logarithm of 2: τ = half-life/[ln(2)] = 1.0/.693 = 1.44 hours The mean lifetime τ is the amount of time it takes for the water to fall to 1/e of its previous level, the "1/e"-life of the bucket. The decay rate λ is the inverse of the mean lifetime τ: λ = 1/τ = 1/1.44 = 0.693 per hour (For a description of the decay constant and half-life, see the Wikipedia article on exponential decay.) If you start with an empty bucket, the amount grows exponentially and approaches the equilibrium level of 40% full: x(t) = x(final) - x(final) e -λt So the bucket starts out empty at t=0, reaches 20% full in one half-life, 30% full in two half-lifes, 35% full in three half-lifes, and so on, approaching 40% full as the elapsed time gets very large. If you start with a 100% full bucket instead, it starts by leaking at 10 drops per second. With 4 drops entering per second, the net loss is 6 drops per second, and the amount in the bucket falls exponentially to the equilibrium level of 40% full: x(t) = x(final) + [2.5*(x(final)) - x(final)] e -kt In this case, the bucket starts out 100% full at t=0, falls to 70% full in one half-life, 55% full in two half-lifes, and so on, again approaching 40% full as the elapsed time gets very large. |
Dripping Bucket = Radioactive Decay Product
Now what has all this dripping have to do with radioactive decay? The water in the huge water tank is like uranium-238, a long-lived nuclide with a tiny decay constant. The water in the bucket is like thorium-234, the immediate decay product of uranium-238. If you extract the uranium chemically from its ore, you separate it from its decay products. After extraction, the uranium-238 immediately begins decaying into thorium-234. The throrium-234 accumulates, quickly at first, then not so quickly, and then slowly approaches its equilibrium amount.
The half-life of thorium-234 is 24 days, so after that many days has passed, the thorium-234 accumulates to one-half of its equilibrium amount. After 48 days, it accumulates to three-fourths of its equilibrium amount, and after 72 days, to seven-eights the final amount, and so on. By the time a few months have passed, thorium-234 reaches its equilibrium amount and decays at the same rate that it is produced by its uranium-238 source.
How much is the equilibrium amount of thorium-234 relative to the amount of the parent nuclide, uranium-238? It is simply the ratio of the half-lifes of the two nuclides. The half-life of uranum-238 is 4.47 billion years, and that of thorium-234 is 24.1 days, After you convert the time units to a common base (left as an exercise for the reader), you find that the half-life of thorium-234 is only 1.48 x 10-11 that of uranium-238. Therefore, under equilibrium, the number of thorium-234 atoms is 1.48 x 10-11 times the number of uranium-238 atoms.
| For the Mathematically Inclined Problem: A sample of uranium contains 1.00 gram of uranium-238. The uranium was extracted from its ore more than a year ago, so it is in equilibrium with thorium-234. How many grams of thorium-234 are present in the sample? Solution: Under equilibrium conditions, the number of uranium-238 atoms multiplied by 1.48 x 10-11 (the ratio of the two nuclide half-lifes) gives you the number of thorium-234 atoms. (1.00 gram U-238) x (1 mole U-238 / 238 grams U-238) (6.02 x 1023 atoms U-238 / mole U-238) x (1.48 x 10-11 atoms Th-234 / atoms U-238) x (1 mole Th-234 / 6.02 x 1023 atoms Th-234) x (234 grams Th-234 / mode Th-234) = (1.00) x (1.48 x 10-11) x (234/238) gram Th-234 = 1.46 x 10-11 gram Th-234 |
The Next Containers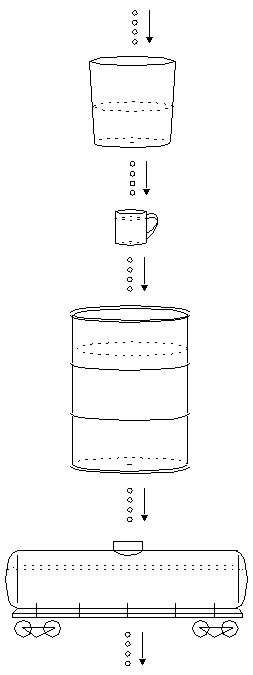
Let's get back to the dripping bucket story. Now that the bucket is 40%
full and dripping just as fast as the water tank, you find another
container, a tin cup, to catch the drips from the bucket. This works
fine for awhile, but soon you find that it too has a
small hole in the bottom. As the cup fills up, it starts leaking faster
and faster. When it's almost full, it's dripping at the same rate as
the water tank and the bucket, 4 drops per second. You need a big container to catch all these drips. So you go next door and find a 55-gallon barrel. You place it under the tin cup. That should take care of the problem!
The next day, you come back and find that the barrel is about one-third full, and unfortunately, it must have a tiny hole in the bottom, because it's leaking a couple of drops per second. The next day, the barrel is about half full and dripping at about 3 drops per second. After several days, the barrel is about 3/4 full and dripping at 4 drops per second.
You decide to take care of this once and for all. You put a railroad tank car beneath the barrel! This works fine for quite a long time. But after a few months, you notice a slow drip from the bottom of the tank car. By the time a year has passed, the tank car is about one-third full and dripping at about 2 drops per second.
So you get another container, and so on. The containers are different shapes and sizes. Sometimes it's just a thimble-sized container with a big hole, which fills quickly. Sometimes it's like the railroad tank car, very large and with a tiny hole, taking years to fill up. But in every case, after you wait long enough, water enters and leaves each container at 4 drops per second.
Eventually, you find a container that doesn't leak at all, ending the long chain of containers. As time passes, all of the containers fill up to their respective equilibrium levels, and all have water entering at a rate of 4 drops per second, and all of them leak at 4 drops per second, except for the very last container at the bottom, which accumulates water at 4 drops per second endlessly.
Uranium-238 Decay Chain
This string of containers is like the uranium-238 decay chain. One gram of uranium-238
decays at a rate of 12,300 atoms per second. In a uranium ore rock
containing one gram of uranium-238, which has been left undisturbed for
millions of years, all of the nuclides in the decay chain have accumulated to
their secular equilibrium levels, such that each nuclide is produced at a rate of
12,300 atoms per second and decays at 12,300 atoms per second. At the
end of the chain is lead-206, a stable isotope that accumulates
continuously at 12,300 atoms per second. The following table shows the amount of each decay-chain product existing in an old uranium ore rock, relative to the amount of uranium-238 present in the rock. For each decay-chain product, the "Mass present" is calculated as the half-life of the nuclide divided by the half-life of the ancestor uranium-238, multiplied the ratio of the atomic masses of the nuclide and uranium-238.
Uranium-238 Decay Chain in an Undisturbed Uranium Ore Rock
| Nuclide | Half-life |
Mass present (relative to ancestor U-238) |
Decay product |
|---|---|---|---|
| uranium-238 | 4.47 billion years |
1.00 |
thorium-234 |
| thorium-234 | 24.1 days | (1.48 x 10-11) x (234/238) | protactinium-234 |
| protactinium-234 | 1.16 minutes | (4.93 x 10-16) x (234/238) | uranium-234 |
| uranium-234 | 245,500 years |
(5.49 x 10-5 ) x (234/238) | thorium-230 |
| thorium-230 | 75,380 years |
(1.69 x 10-5 ) x (230/238) | radium-226 |
| radium-226 |
1602 years |
(3.58 x 10-7 ) x (226/238) | radon-222 |
| radon-222 | 3.82 day |
(2.34 x 10-12) x (222/238) | polonium-218 |
| polonium-218 |
3.10 minutes | (1.32 x 10-15) x (218/238) | lead-214 |
| lead-214 |
26.8 minutes | (1.14 x 10-14) x (214/238) | bismuth-214 |
| bismuth-214 |
19.9 minutes | (8.47 x 10-15) x (214/238) | polonium-214 |
| polonium-214 |
0.164 msec | (1.16 x 10-21) x (214/238) | lead-210 |
| lead-210 |
22.3 years |
(4.99 x 10-9 ) x (210/238) | bismuth-210 |
| bismuth-210 |
5.01 days |
(3.07 x 10-12) x (210/238) | polonium-210 |
| polonium-210 |
138 days | (8.46 x 10-11) x (210/238) | lead-206 |
| lead-206 |
stable | Depends on age of rock |
-- |
What Happens When You Empty the Containers (Extract the Uranium)? 
When uranium is extracted chemically from its ore, it is separated from
its decay products. How much of each decay product is produced by pure
uranium after it's extracted? For the time being, let's ignore the small amount of uranium-234
and uranium-235 in the rock, and assume that all the uranium freshly
extracted from its ore is pure uranium-238. In that case, uranium
extraction is like emptying all the containers below the
water
tower, and starting with a fresh set of empty containers. At first, water drips into the bucket at the top, and nothing else happens. As the bucket starts filling up, it starts dripping into the tin cup. After the cup starts filling up, it starts dripping into the barrel, and so on. The containers fill up in sequence, starting with the top containers, and gradually trickling down to the lower containers. A large, slow container such as a railway tank car creates a bottleneck in the chain, causing all the containers below it to remain empty for a long time.
In the case of uranium-238, the initial bucket in the chain is thorium-234, which has a half-life of 24 days. So 24 days after pure uranium is extracted from its ore, the amount of thorium-234 reaches one-half its equilibrium level, and is dripping into the next container, the "tin cup," protactinium-234, at half the equilibrium rate. Protactinium-234 has a half-life of just 1 minute, so it empties almost immediately into the "barrel," uranium-234. Uranium-234 has a half-life of 245,000 years, so on a human time scale, it can be considered a stable end product. True secular equilibrium for the entire chain takes at least a million years. For a detailed accounting of the decay rates of natural uranium, see Calculation of Decay Activity of One Gram of Natural Uranium.
What Happens When You Move the Containers Aside (Examine the Mining Waste)?
You might be surprised to learn that in a uranium ore rock, the ancestor
nuclide, uranium-238, contributes only a small fraction of the total
radioactivity of the rock. Most of the radioactivity comes from the
decay-chain products, not from the uranium-238 itself. If you look at
the whole decay chain under secular equilibrium conditions, each drip from each container
in the chain represents a radioactive decay, each releasing an amount
of energy similar to each of the other drips in the chain. Since
there are 14 dripping containers
(including the municipal water tank), the decay of the ancestor
uranium-238 nuclide contributes only one-fourteenth of the total
radioactivity of the rock. Separating uranium-238 from its ore is like taking a set of dripping containers under secular equilibrium conditions, moving them aside, and putting a new string of empty containers beneath the water tank, as shown in the picture on the left.
The water tower and its empty containers represent the extracted urnaium-238, while the string of full containers on the right represents the discarded mining waste. The moved-over set of full containers continue to drip, while the municipal water tower starts dripping into the first container, the bucket. Initially, on the left there are only 4 drops per second entering the empty bucket on the top, but on the right, all the containers are dripping at 4 drops per second. The mining waste is 13 times more radioactive than the uranium-238 itself.
What happens over time? On the left, as the bucket on the left starts filling up, it stars dripping into the tin cup, and as the tin cup starts filling up, it starts dripping into the next container, and so on. On the right, as the top bucket's water level drops, the drip rate into the tin cup starts slowing down, causing the water level to drop in the tin cup, and the drip rate from the tin cup starts slowing down, and so on.
On the left, the bucket at the top eventually fills up to its equilibrium level, and feeds the tin cup at its equilibrium rate. On the right, the bucket at the top eventually empties completely, and stops feeding the tin cup entirely.
As it turns out, all the actions on the left and right are exactly complementary. As each container on the left fills up, the water level in the corresponding container on the right drops by the same amount. If you combine the water from the left bucket and the right bucket at any given time, the total amount of water will be the equilibrium amount for the bucket. This is true for the tin cup, the barrel, and and all the other containers in the chain. Eventually, all the containers on the left fill up and all the containers on the right become empty, starting from the top and trickling down (or emptying down) the chain of containers.
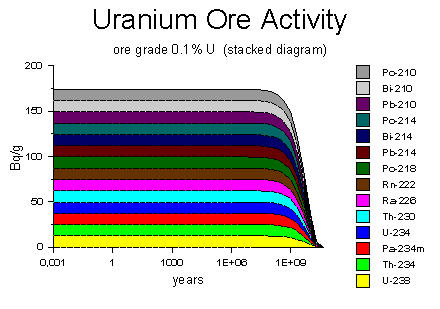
The diagram on the right shows the decay activity of a one-gram uranium ore rock containing 0.1% uranium on a logarithmic time scale, ranging from 3 days to 30 billion years. The colored bars represent the decay activity of the uranium-238 and each of its decay-chain products in the rock. Because the rock is in secular equilibrium, all of the decay products have the same decay rate of 12 atoms per second. Eventually, after many billions of years, the uranium-238 will run out and the decay will diminish to nothing.
You might wonder why the activity appears to remain constant for such a long time, and then falls off rapidly. It's because of the logarithmic time scale. During the first 50 million years, the activity falls less than 1%, so that part of the graph looks constant. A linear time scale would show the classic exponential decay curve.
Source of diagram: WISE Uranium Project, Uranium Radiation Properties
Compare the activity of uranium ore with the activity of one gram of natural uranium extracted from its ore and one gram of uranium mining waste (mill tailings), below.
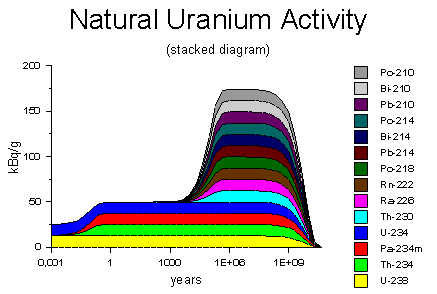
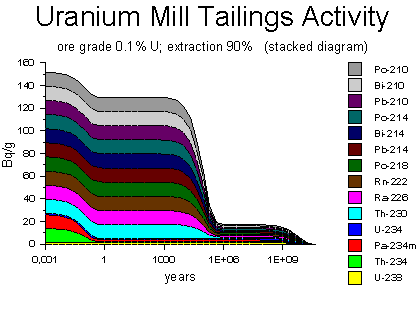
Source of decay activity diagrams: WISE Uranium Project, Uranium Radiation Properties
The natural uranium extracted from its ore initially consists of uranium-238 (yellow) and a tiny amount of its third-level decay product, uranium-234 (blue), both decaying at a rate of 25 kBq. Uranium-238, within a few months, produces its equilibrium amount of thorium-234 and protactinium-234; it fills up its bucket and tin cup to their equilibrium levels. The uranium-234 starts producing thorium-230, but the latter has a half-life of 75,000 years, so it takes many thousands of years to accumulate to significant levels. Eventually, after about half a million years, the uranium reaches secular equilibrium, just like an old uranium ore rock. After many billions of years, the supply of uranium-238 runs out, and the activity declines to nothing.
In the mining waste discarded after uranium extraction, the decay-chain products are present and decaying. The products at the top of the chain, thorium-234 and protactinium-234 (yellow and red), run out after a few months; the bucket and tin cup are completely emptied. The remaining decay-chain elements continue to be supplied for a long time by the thorium-234, which has half-life of 75,000 years. Eventually, after about half a million years, the thorium runs out, and the decay rate diminishes to nothing. (In the Uranium Mill Tailings Activity diagram above, there is still a small amount of residual activity after half a million years because of the 10% of uranium-238 that was left behind during the 90%-efficient extraction process.)
Like the empty and full strings of containers below the water tank, the decay activity of the uranium and its extracted mining waste are complementary. As the activity of the extracted uranium increases, the activity of the mining waste decreases by a like amount.
This seemingly peculiar behavior of a radioactive elements and their decay products led to the discovery of the nature of radioactivity itself. When Ernest Rutherford and Frederick Soddy examined the behavior of radium and its decay products (which have laboratory-observable half-lives), they deduced from this behavior the random nature of radioactive decay. For the whole story of this discovery, see Soddy's book The Interpretation of Radium and the Structure of the Atom.
Radioactive Decay Problem Examples